In my previous blog post I showed how to solve Takuzu puzzles using SQL. After writing that post I couldn’t stop wondering what other puzzles could be (somewhat elegantly) expressed and solved using SQL. I realized that the classic wolf, goat, and cabbage puzzle would be a good candidate. Its search space is very small and with a suitable state and action representation the SQL code isn’t too incomprehensible.
So what’s this puzzle about?
The puzzle goes like this:
A farmer needs to cross a river, bringing with him a wolf, a goat, and a cabbage. The boat is small, so the farmer can only take one of the three with him at a time. The difficulty comes from the fact that certain pairs can’t be left alone. If the wolf is left with the goat, the wolf will eat the goat. If the goat is left with the cabbage, the goat will eat the cabbage. Only the farmer’s presence prevents these things from happening.
You may want to try to solve by hand first before reading on. It’s not that hard.
The solver
This is what I came up with:
WITH RECURSIVE
moves(mask, move_desc) AS (
VALUES
(1, "Farmer crosses alone"),
(3, "Farmer takes wolf"),
(5, "Farmer takes goat"),
(9, "Farmer takes cabbage")
),
states(i, visual) AS (
SELECT 0, '👨 🐺 🐐 🥬 | 🚣🌊🌊🌊🌊 |'
UNION ALL
SELECT
i + 1,
(CASE (i+1>>0)&1 WHEN 0 THEN '👨 ' ELSE ' ' END) ||
(CASE (i+1>>1)&1 WHEN 0 THEN '🐺 ' ELSE ' ' END) ||
(CASE (i+1>>2)&1 WHEN 0 THEN '🐐 ' ELSE ' ' END) ||
(CASE (i+1>>3)&1 WHEN 0 THEN '🥬 ' ELSE ' ' END) ||
(CASE (i+1>>0)&1 WHEN 0 THEN '| 🚣🌊🌊🌊🌊 | ' ELSE '| 🌊🌊🌊🌊🚣 | ' END) ||
(CASE (i+1>>0)&1 WHEN 1 THEN '👨 ' ELSE ' ' END) ||
(CASE (i+1>>1)&1 WHEN 1 THEN '🐺 ' ELSE ' ' END) ||
(CASE (i+1>>2)&1 WHEN 1 THEN '🐐 ' ELSE ' ' END) ||
(CASE (i+1>>3)&1 WHEN 1 THEN '🥬 ' ELSE ' ' END)
FROM states
WHERE i < 15
),
explore(state, path, actions) AS (
-- start
SELECT 0, '0', printf('%-20s | %s', 'Start') || visual FROM states WHERE i = 0
UNION ALL
SELECT
state + mask - 2*(state & mask) AS next_state,
path || ' -> ' || (state + mask - 2*(state & mask)),
actions || char(10) || printf('%-20s | %s', move_desc) || visual
FROM explore, moves, states
WHERE
-- join with states CTE for visuals
state + mask - 2*(state & mask) = i
-- farmer must be with passenger (unless alone)
AND (mask = 1 OR ((state & 1) = (state & mask) / mask))
-- avoid revisiting states
AND instr(path, state + mask - 2*(state & mask)) = 0
-- wolf + goat unsafe
AND NOT (
((state + mask - 2*(state & mask)) >> 1 & 1)
= ((state + mask - 2*(state & mask)) >> 2 & 1)
AND ((state + mask - 2*(state & mask)) >> 0 & 1)
!= ((state + mask - 2*(state & mask)) >> 1 & 1)
)
-- goat + cabbage unsafe
AND NOT (
((state + mask - 2*(state & mask)) >> 2 & 1)
= ((state + mask - 2*(state & mask)) >> 3 & 1)
AND ((state + mask - 2*(state & mask)) >> 0 & 1)
!= ((state + mask - 2*(state & mask)) >> 2 & 1)
)
)
SELECT
group_concat(actions, char(10) || char(10))
FROM (
SELECT actions
FROM explore
WHERE state = 15
);The first two CTEs define the static parts of the problem: all possible moves and all possible states. The third CTE performs a recursive search over the state space, applying moves and filtering out invalid transitions.
State and action representation
The query is kept small thanks to the bitmask representation of state and action.
Each entity is represented by one bit:
| Bit | Entity |
|---|---|
| 0 | Farmer |
| 1 | Wolf |
| 2 | Goat |
| 3 | Cabbage |
If a bit is 0, it means the entity is on the left bank, and a 1 means right bank. Using this representation the state is a number from 0 to 15:
| Decimal | Binary | Meaning |
|---|---|---|
| 0 | 0000 | Everything including the farmer is on the left bank |
| 5 | 0101 | Farmer and goat are on the right |
| 15 | 1111 | Everything including the farmer is on the right bank |
The goal state is simply 15.
Moves are represented using the same bitmask scheme.
| Move | Mask | Binary |
|---|---|---|
| Farmer alone | 1 | 0001 |
| Farmer and wolf | 3 | 0011 |
| Farmer and goat | 5 | 0101 |
| Farmer and cabbage | 9 | 1001 |
Applying a move (the farmer moving from one side of the river to the other, either alone or with one entity) means flipping those bits (using XOR).
Since SQLite doesn’t have XOR, we rewrite XOR as:
state + mask - 2*(state & mask)which has the same effect.
The WHERE part in the CTE explore checks whether after applying a move, the wolf and goat, or the goat and cabbage, aren’t left unsupervised.
Running the query
Running the query produces the following output:
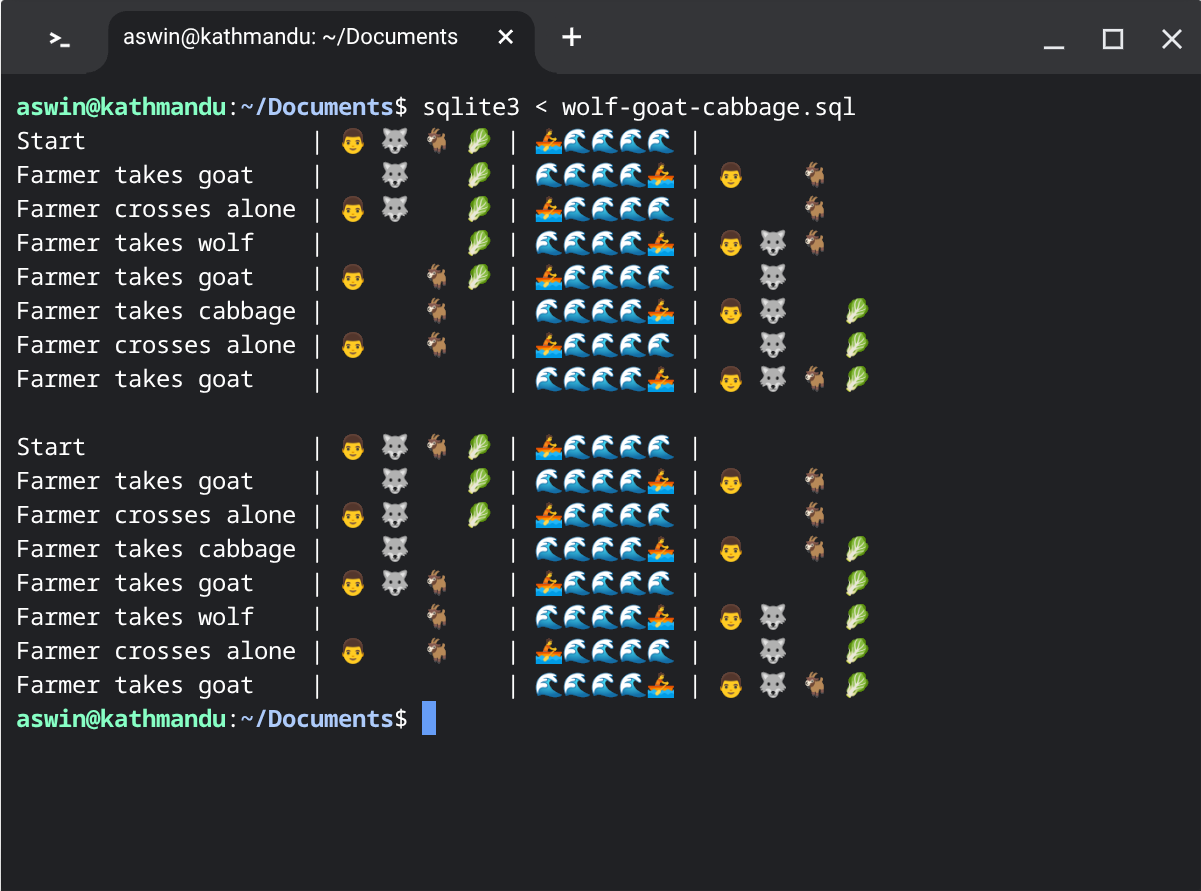
There are infinitely many solutions (as the farmer can just row back and forth), but the solver only outputs the two shortest ones. The solver does this by making sure that previously visited states aren’t repeated. Emojis are used to visualize the state after each action.
You can find the query as a gist here: